Where do properties come from?
A not-infrequent response to my skeptical essay on property-based-testing (PBT) is that I left out an important benefit: it makes you think about properties. (I think "invariant" would be a more precise word, but I'll stick with the standard "property".)
That response appeals to me a lot, since it's parallel to what people like me say about test-driven design: that design is the most important word, and that "listening to tests" shapes design.
Let's look more closely at creating properties.
Euler's property
Euler famously discovered a property of polyhedra (cubes, etc.). No matter what the inputs to an imaginary polyhedron-making program, every polyhedron generated will satisfy the property V - E + F = 2, where V is the number of vertices, E is the number of edges, and F is the number of faces. A cube has 8 vertices, 12 edges, and 6 faces, so a Polyhedron-Based Testing tool would find the property always holds.
Except, well, it sort of doesn't...
One of my favorite books, Imre Lakatos's Proofs and Refutations, discusses the history of Euler's property. It's interesting because people can, and did, discover polydedra for which Euler's property didn't hold, even though he had proven it correct (though not rigorously, by today's standards).
Here, via harveycohen.net, are three refutations of Euler's property:
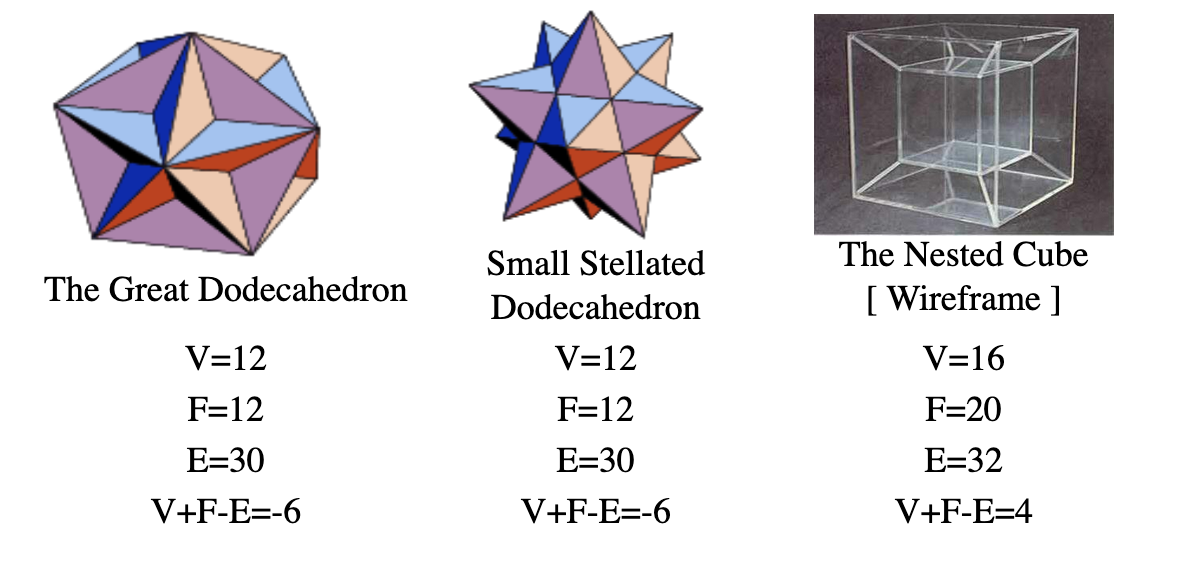
At this point, you should code up a polyhedron-generating program (let's call it poly ), apply random inputs to it, and see if any of these buggy shapes (Lakatos called them "monsters") are discovered.
More likely, in my mind, would be that the knowledge of Euler's property would incline you to write a poly that produced only polyhedra that satisfied the property. But that's the wrong way 'round. What Euler wanted to do was to find a property true of all polyhedra. He found one true of some polyhedra and mistakenly assumed it was true of all of them.
The problem was he didn't fully understand the "business domain." Lakatos's history of Euler's property shows generations of mathematicians using counterexamples to more fully understand the different kinds of polyhedra, what their properties are, and how those properties relate to other types of mathematics.
The lesson I take from Lakatos is that properties (generalizations, abstractions, etc.) are fine, but they must often go through a process of refinement, that refinement is largely driven by counterexamples, and counterexamples are found by people making a purposeful search through the space of possible inputs, guided by earlier results.
In the terminology of the last essay, mathematicians were looking for the small red partitions in the space of three-dimensional figures with vertices, faces, and edges.
Glass's evidence
In 1981, Robert Glass wrote a paper based on analysis of bugs found in production aviation software. His "Persistent Software Errors" found that the most important class of bugs was "code not as complex as required by the problem." Back in the later 1980's, I did a literature search: his company's experience was not an outlier. Yet this huge elephant in the room is rarely talked about.
Most of Glass's bugs were the failure to include branching logic, such as failing to write absolute_value(x) instead of x . (In this case, the branch hides inside the definition of absolute_value.)
Now, the simplistic solution to such problems is to just add a whole bunch of special-case branching. But it's also the experience of a lot of programmers that sometimes the proliferation of special cases – Lakotosian monsters – collapses into a new, better abstraction (much as counterexamples to Euler's property led to the abstraction of a convex polyhedron).
We don't want such Aha! design moments to be driven by production bugs (especially in avionics software!). So, the question is: how can such understandings be found earlier?
My suggestion is: not by focusing on properties, but rather by being methodically obsessive about working with counterexamples.
Test-driving properties
The red-green-refactor loop of test-driven design can be looked at from combined Glass/Lakatos perspective as:
- Produce a counterexample that shows the code is not complex enough for the problem.
- Add the complexity.
- Ask if you've learned of any new properties/abstractions or if your understanding of existing ones has changed. If so, put that understanding to work in the code.
Bill Wake has written a fair amount on this topic.
I expect, but cannot prove, that a TDD approach will produce better – more appropriate – properties than will a less-structured approach, especially one that pushes you toward creating properties as a single, preliminary step.
An argument-by-analogy is that, just as probing at Euler's polyhedron property helped lead to the more broadly-useful notion of the Euler characteristic in algebraic topology, the probing of TDD will lead to better properties/invariants.
Self-criticism session
The weak point in my argument above is that I've mushed together a claim that TDD leads to better abstractions with a claim it will lead to a better understanding of properties. To the extent that properties are phrased in terms of abstractions (like "lines", "edges", and "vertices") that seems... plausible? But I don't have the experience to know if it's true even just for me. If you have extensive experience with both TDD and PBT, please comment.
Something of an example
Recently I worked out Hillel Wayne's PBT / Example Testing comparison problem. I'll quote enough of it that you won't have to click through to understand.
You are writing simple budgeting software. A Budget consists of a total limit, represented as a positive integer, and a dictionary of category limits, represented as a map from strings to integers. For example:
{"total_limit": 50,
"category_limits": {
"food": 10,
"rent": 11,
"candles": 49
}
}[...]
A Bill is an array of Items. Each Item has a cost (positive integer), an optional count (positive integer), and optional categories (array of strings). For example:
[
{"cost": 5},
{"cost": 1, "count": 3},
{"cost": 2, "categories": ["food", "gym"]},
{"cost": 1, "count": 2, "categories": ["transit"]}
]The goal is to write can_afford(budget, bill).I implemented my solution using TDD in the traditional way. It's a small problem, but some annoyance at what seemed like duplicate work prompted me observe that the whole is a variant of the part:
- Looking at the above example,
{"total_limit": 50}has the same "shape" as{"food": 10, ...}. Call such shapesLimitHolders. - The processing of the
total_limitseems different from the individual category processing, but it could be identical if you considered every bill item to have an implicit"total_limit"category.
I'd written total-limit processing before starting on categories. In the end, I decided changing that code to use a LimitHolder was more trouble than it's worth, but perhaps that means a property derived from LimitHolder would be extra-special-good at testing the "total_limit" calculations?
More research is needed
If you have experience with PBT, I'd be happy to collaborate with you.
One question I'm interested in: if you use TDD to incrementally develop tests, code, abstractions, and properties, what additional value does randomization add?